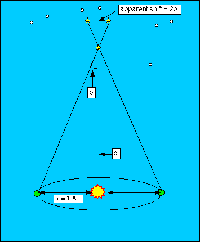
 Distances in the universe are so vast that we do not have a simple way of measuring them. For distances within the solar system we can measure them directly, using radar for example, and some very straightforward trigonometry. But radar is hard to use when it takes light minutes or hours to cross the solar system; and the nearest star is four light years away! A more difficult but straightforward method is trigonometric parallax, the derivation of distances to nearby stars by measuring by how much they appear to shift relative to background stars during the course of a year. This method is the most direct way that we have of measuring the distances to the stars, but only for those within about a thousand light years. The measurement of parallaxes requires very precise measurements of the positions of stars on the sky. The largest parallax -- that of alpha Centauri -- is less than one arcsecond, and that is the closest star to us (4.3 light years away). For comparison, the full moon is 1800 arcseconds across! The size of the parallax decreases the farther away the star is, until eventually it is smaller than we can measure.
Distances in the universe are so vast that we do not have a simple way of measuring them. For distances within the solar system we can measure them directly, using radar for example, and some very straightforward trigonometry. But radar is hard to use when it takes light minutes or hours to cross the solar system; and the nearest star is four light years away! A more difficult but straightforward method is trigonometric parallax, the derivation of distances to nearby stars by measuring by how much they appear to shift relative to background stars during the course of a year. This method is the most direct way that we have of measuring the distances to the stars, but only for those within about a thousand light years. The measurement of parallaxes requires very precise measurements of the positions of stars on the sky. The largest parallax -- that of alpha Centauri -- is less than one arcsecond, and that is the closest star to us (4.3 light years away). For comparison, the full moon is 1800 arcseconds across! The size of the parallax decreases the farther away the star is, until eventually it is smaller than we can measure.
Beyond this point, we have to start relying not just on observation but also on our understanding of astrophysics. As an example, after parallaxes we can use open clusters -- groups of stars formed at the same time having the same ages but different masses, temperatures, and luminosities -- to make educated guesses as to the absolute brightnesses (and hence distances) of the cluster members. We calibrate those guesses using clusters for which we can measure parallaxes, and then extend them outwards to where we can't measure parallax. Our understanding of the size of the universe is dependent upon The Cosmic Distance Ladder, a series of measurements of different kinds of objects and phenomena, each building upon the previous step in the ladder. By extending the ladder with different kinds of measurements (and intelligent guesses), we can measure larger and larger distances in the universe.
Several of these steps are critically dependent upon variable stars, and the physical study of the Distance Ladder is in some ways a physical study of variable stars. How have variable stars contributed to the Distance Ladder, and why? Here, we'll discuss two of them: the Period-Luminosity relation of pulsating stars, and the use of Type Ia supernovae as standard candles.
The Leavitt Law: Cepheid variables as distance indicators
 Harvard Astronomer Henrietta Swan Leavitt made a critical observation about Cepheid variables observed in the Small Magellanic cloud. After measuring the periods of the Cepheids and the relative brightnesses of each, she found a relation between the period and apparent brightness for all of the stars; the stars with longer periods were brighter than those with shorter periods. Making the reasonable assumption that the Small Magellanic Cloud is far enough away that all the stars are at approximately the same distance, you can assume that there is a relation between the period and the absolute brightness as well. This was a critically important discovery in modern astrophysics; it meant that one could make an easy measurement -- the pulsation period of the Cepheid -- and obtain the distance, which is otherwise impossible to obtain.
Harvard Astronomer Henrietta Swan Leavitt made a critical observation about Cepheid variables observed in the Small Magellanic cloud. After measuring the periods of the Cepheids and the relative brightnesses of each, she found a relation between the period and apparent brightness for all of the stars; the stars with longer periods were brighter than those with shorter periods. Making the reasonable assumption that the Small Magellanic Cloud is far enough away that all the stars are at approximately the same distance, you can assume that there is a relation between the period and the absolute brightness as well. This was a critically important discovery in modern astrophysics; it meant that one could make an easy measurement -- the pulsation period of the Cepheid -- and obtain the distance, which is otherwise impossible to obtain.
 While stars in the Magellanic cloud are much too far away to measure distances using parallax, there are enough well-calibrated, in-between steps in the Distance Ladder to let you calibrate the Cepheid Period-Luminosity relation for nearby Cepheids. The PL relation has become one of the most critically important tools for distance measurement in the cosmos. Leavitt's 1908 discovery was confirmed to work not only for Cepheids but for a number of other pulsating variables as well. One of these types were the RR Lyrae stars commonly found in globular clusters, and measurement of distances to the globular clusters formed part of the argument that allowed astronomers to finally understand the size and shape of the Milky Way galaxy and all other "spiral nebulae" in the universe. One measurement changed the our understanding of the size of the universe by many orders of magnitude -- from thousands of light years to millions (and eventually to billions).
While stars in the Magellanic cloud are much too far away to measure distances using parallax, there are enough well-calibrated, in-between steps in the Distance Ladder to let you calibrate the Cepheid Period-Luminosity relation for nearby Cepheids. The PL relation has become one of the most critically important tools for distance measurement in the cosmos. Leavitt's 1908 discovery was confirmed to work not only for Cepheids but for a number of other pulsating variables as well. One of these types were the RR Lyrae stars commonly found in globular clusters, and measurement of distances to the globular clusters formed part of the argument that allowed astronomers to finally understand the size and shape of the Milky Way galaxy and all other "spiral nebulae" in the universe. One measurement changed the our understanding of the size of the universe by many orders of magnitude -- from thousands of light years to millions (and eventually to billions).
Why does this relation exist? One way to think about it is to consider why stars have different intrinsic brightnesses. The amount of light a star will give off is dependent on two things: its physical size, and its temperature. Cepheids lie in a fairly narrow range of temperatures, and so the primary difference between one Cepheid and another is its size. You can prove, using simple dynamical arguments, that the amount of time it takes a star to complete one pulsation cycle is directly proportional to the size of the star -- the bigger the star, the longer it takes for it to complete a pulsation cycle. But since we know bigger stars are more luminous, then we can determine a relation between the period and the luminosity.
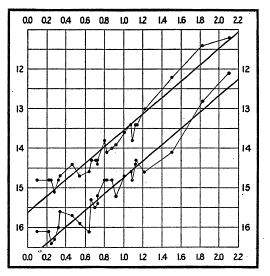
Folded visual light curves of two Cepheids, SV Vul and T Vul. The period of SV Vul is about 10 times longer than that of T Vul. If they were the same distance from us, T Vul would appear to be fainter than SV Vul; since it is not (T Vul is about 1.5 magnitudes brighter at maximum), it must be much closer.
We've used the period-luminosity relation to measure distances to Cepheids in the Milky Way, the local Group, and out to galaxies about 60 million light years distant (M100 is the most distant galaxy with measured Cepheids). We continue to refine and recalibrate the Cepheid period-luminosity relation as we get better data, but distances obtained with it are probably good to around five percent. Thus we have a good measure of the distances to nearby galaxies. Critically, we can then use Cepheids to calibrate another rung of the distance ladder, redshifts. Using Cepheids, we can obtain measures of distances to nearby galaxies with redshifts showing a clear direct relationship between distance and redshift. Redshifts are in turn used to measure distances of hundreds of millions or billions of light years, rather than the tens of millions possible with Cepheid variable observations.
In recognition of Henrietta Swan Leavitt's discovery of and early work on the period-luminosity relation, the Cepheid P-L relation is now referred to as the Leavitt Law. It was one of the most important astrophysical discoveries of the 20th Century, but it may not be the most important discovery in the story of the Cosmic Distance Ladder. That distinction might go to what we talk about next.
Type Ia Supernovae, Dark Energy, and the Acceleration of Cosmic Expansion
Those who measure distances in the universe often use the term "standard candle" as a metaphor for a calibrated light source in a distant target. In order to measure large distances you need a very, very bright candle. The supernovae are among the brightest variable stars there are, and we can see supernovae in galaxies hundreds of millions of light years distant. There are a number of different types of supernovae, but they originate primarily from two different types of progenitors: the collapse and subsequent explosion of massive white dwarf stars in cataclysmic variable binary systems, and the collapse of massive stars at the ends of their lives. The most interesting systems for the current discussion are the collapsing white dwarf systems, known as supernovae of "Type Ia".
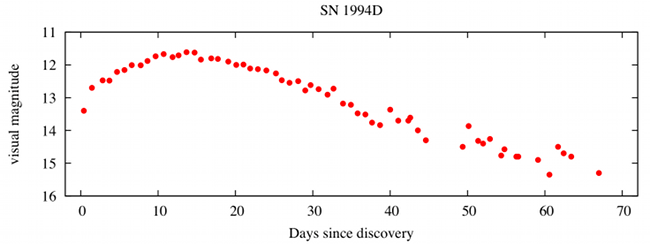
One-day averages of visual observations of the Type-Ia supernova SN 1994D (discovered March 9, 1994).
In Type Ia supernovae, a white dwarf in a binary system is accreting matter from the secondary star of the binary. White dwarfs have limits on how massive they can be (about 1.4 times the mass of the Sun), which is known as the Chandrasekhar limit after its discoverer, Subramanyan Chandrasekhar. If a white dwarf becomes more massive than this (by accreting matter from a companion, for example) then the atomic forces that hold the star up against gravity can no longer support the weight of the outer layers and the star collapses. In so doing, the core of the star undergoes violent nuclear reactions that generate an enormous amount of energy, and the star explodes, disrupting it entirely. Since all type Ia supernovae are caused by the same physical process, type Ia supernovae behave in roughly the same way and release the same amount of energy when they explode. This is exactly what one needs when looking for a standard candle. And better still, type Ia supernovae are bright, and can outshine all of the other stars in a galaxy combined. You can detect supernovae in galaxies hundreds of millions of light years distant, giving us a powerful tool for calibrating redshifts at larger distances than Cepheids can.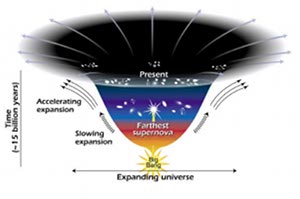 But now the story gets interesting. In the late 1990's, there were two independent teams of astronomers trying to find and record type Ia supernovae in distant galaxies as part of a larger study trying to understand the fundamental nature of the cosmos. It was assumed that the relationship between redshift and the peak brightness of supernovae should be constant since it was also assumed that the expansion of the universe has been constant since the big bang. However, the two teams discovered that type Ia supernovae at higher redshifts were fainter than one would expect from this constant expansion, meaning they were further away. This implies that the universe has not been expanding at a constant rate, but is accelerating. This is the first observational hint of the existence of something called "dark energy", something predicted by Albert Einstein but whose cause and origin remains largely unknown. If dark energy is real -- and multiple lines of cosmological evidence are pointing toward that conclusion -- it represents a fundamental reworking of our understanding of the universe, its origins, and its ultimate fate. While the Leavitt Law represented a new way to measure the size of the Universe, the measurement of cosmic acceleration might bring about an entirely new understanding of cosmology.
But now the story gets interesting. In the late 1990's, there were two independent teams of astronomers trying to find and record type Ia supernovae in distant galaxies as part of a larger study trying to understand the fundamental nature of the cosmos. It was assumed that the relationship between redshift and the peak brightness of supernovae should be constant since it was also assumed that the expansion of the universe has been constant since the big bang. However, the two teams discovered that type Ia supernovae at higher redshifts were fainter than one would expect from this constant expansion, meaning they were further away. This implies that the universe has not been expanding at a constant rate, but is accelerating. This is the first observational hint of the existence of something called "dark energy", something predicted by Albert Einstein but whose cause and origin remains largely unknown. If dark energy is real -- and multiple lines of cosmological evidence are pointing toward that conclusion -- it represents a fundamental reworking of our understanding of the universe, its origins, and its ultimate fate. While the Leavitt Law represented a new way to measure the size of the Universe, the measurement of cosmic acceleration might bring about an entirely new understanding of cosmology.
Variable Stars help tell the story
Distance measurement in the universe has been an important advance in astronomical history, and it's not only telling us how big the universe is, but what the universe is fundamentally like and how it will evolve over time. These two classes of variable stars -- pulsating Cepheids and exploding supernovae -- have provided key steps in the Cosmic Distance Ladder. They're just one example of how variable stars have helped to advance the science of astronomy, and taught us more about the cosmos in which we live. It's hard to predict what future advances will be, but it's likely that variable stars will provide many more insights into the nature of our universe.


